0. 계수 정렬 소개
계수 정렬은 O(n)의 시간복잡도를 가지고 있는, 매우 빠른 정렬 방식이다. 또한 숫자가 중복되거나 말거나 상관 없이 같은 속도로 정렬이 가능하다.
하지만, 정렬하고자 하는 배열 외에 (1)문자의 개수를 셀 때 사용하는 배열, (2)새롭게 정렬해야 하는 배열, 이렇게 두개의 배열의 메모리가 더 필요하다. 즉, 매우 큰 수를 정렬하고자 할 때, 그 만큼 큰 용량의 메모리가 필요하다.
이렇게 설명하면 알기 쉽지 않다. 기초부터 한번 알아보자.
1. Key와 Radix

계수 정렬을 이해하기 위해서는 Radix라는 개념을 알아야 한다.
다음 표를 보자. Binary(2진수), Decimal(10진수), Upper/Lower case(대소문자), ascii코드 등, 익숙한 문자들이 많이 보일 것이다.
우리가 알고 있는 대부분의 문자는 "Radix"와 "Key" 로 표현할 수 있다.
여기서 R() 항목의 숫자는, 표현 가능한 숫자의 개수이고 lgR() 항복의 숫자는 log2(N) 값을 나타낸 것이다.
우리가 알고 있는 Ascii(Extended Ascii)값은 2^8 = 256으로서 R() = 256, lgR() = 8 의 값을 가진다.
Radix와 Key의 이해를 위해 10진수와 영어 소문자, ascii 코드로 예시를 들어보자.
Radix와 Key값은 다음과 같이 표현될 수 있다.



2. 계수 정렬 이해하기

다음 간단한 배열을 계수 정렬을 이용해서 정렬 해보자.
총 12개의 숫자로 이루어져 있는 이 배열은
char a[13] = "dacffbdbfbea"
와 같이 설정되어 있다.
이 정렬이 끝나고 나면
[0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11]
a a b b b c d d e f f f
로 정렬이 되어야 한다.
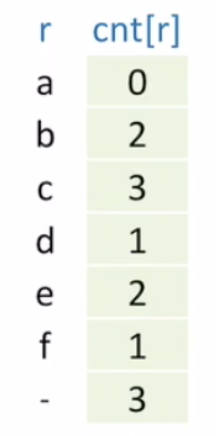
이를 위해 우리는 cnt라는 배열을 선언해야 한다.
cnt는 어떤 문자가 몇개 있는지를 저장하기 위한 배열이다.
그리고 이 배열은 원래 우리가 보았던 R() 값의 크기를 가진다.
지금 이 배열은 a, b, c, d, e, f 원소들을 가지고 있기 때문에 R() 값은 6이다.
하지만, 우리는 indexing을 위해서 한개씩 밀려서 저장을 해보겠다.
즉, a의 개수는 2, b의 개수는 3, c의 개수는 1이지만 다음과 같이 한칸 씩 밀어서 저장을 할 것이다.
이렇게 저장하는 이유는 정렬된 배열에서는 a는 a[0]에서 시작을 하고, b는 a[2]에서 시작을 하고 c는 a[5]에서 시작을 해야 하기 때문이다.
이를 위한 코드는 다음과 같다.
char a[13] = "dacffbdbfbea";
int N = strlen(a); // 문자의 총 개수
int R = strlen("abcdef"); // R() 값
int *count = new int[R + 1]; // 한개씩 밀려서 저장해야 하기 때문에 R() + 1 개수만큼 할당
// 0으로 초기화
for (int i = 0; i <= R; i++)
count[i] = 0;
// key에 해당하는 radix의 [인덱스 + 1] 의 값을 하나씩 늘려준다.
for (int i = 0; i < N; i++)
{
count[a[i] - 'a' + 1]++;
}이 과정이 끝나고 나면, 위의 표와 같이 cnt[r] 배열 안에 값들이 들어가 있을 것이다.
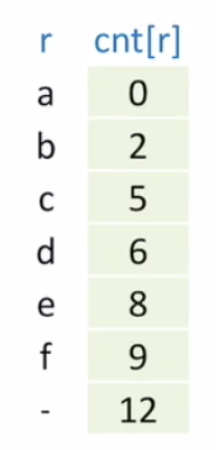
하지만, 아직 불완전한 인덱스를 가진다.
실제로는 a는 a[0]에서 시작을 하고, b는 a[2]에서 시작을 하고 c는 a[5]에서 시작하고, d는 d[6]에서 시작하지만, 아직 각 key값이 몇개를 가지고 있는지만 표현했을 뿐이기 때문이다.
다음과 같이 실제로 각각의 문자들이 배열에서 시작하는 인덱스 값을 부여해주기 위해서는
이를 위해 인덱스들을 더해주어야 한다.
for (int r = 0; r < R; r++)
{
count[r + 1] += count[r];
// 앞에서부터 이전 인덱스를 다음 인덱스에 더해주면 실제 인덱스 값을 부여할 수 있다.
}
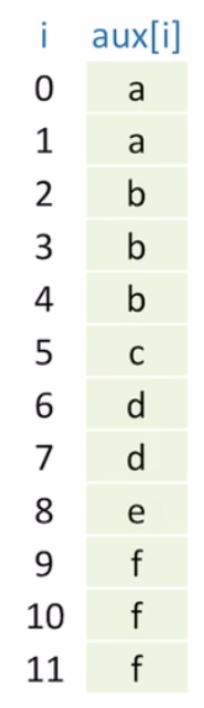
우리는 이제 aux라는 보조 배열을 선언해야 한다. 배열의 크기는 a와 같다.
그리고 우리는 이 배열에 아까 구했던 실제 인덱스 값을 기준으로 문자를 하나씩 넣어줄 것이다.
예를 간단하게 들어보겠다.
지금 정렬되지 않은 배열의 첫번째 문자가 d인데, 이 d는 6의 인덱스 값을 가진다.
(cnt[3] = 6)
그러면 aux[6] = 'd' 가 되는 것이다. 그리고 cnt[3]++ 를 해주면, 다음에 또 d가 들어와야 할 때, aux[7]에 d가 들어갈 수 있게 된다.
마지막으로 보조 배열을 원래 배열에 덮어씌워 주면, 정렬이 끝난다.
코드는 다음과 같다.
char aux[N];
for (int i = 0; i < N; i++)
{
aux[count[a[i] - 'a']] = a[i];
count[a[i] - 'a']++;
}
for (int i = 0; i < N; i++)
a[i] = aux[i];
전체 코드는 다음과 같다.
#include <iostream>
using namespace std;
int main(void)
{
char a[13] = "dacffbdbfbea";
int N = strlen(a);
int R = strlen("abcdef");
int *count = new int[R + 1];
char aux[13];
for (int i = 0; i <= R; i++)
count[i] = 0;
for (int i = 0; i < N; i++)
{
count[a[i] - 'a' + 1]++;
}
for (int r = 0; r < R; r++)
{
count[r + 1] += count[r];
}
for (int i = 0; i < N; i++)
{
aux[count[a[i] - 'a']] = a[i];
count[a[i] - 'a']++;
}
for (int i = 0; i < N; i++)
a[i] = aux[i];
for (int i = 0; i < N; i++)
cout << a[i] << " ";
cout << endl;
}
'알고리즘' 카테고리의 다른 글
| [알고리즘] P, NP (0) | 2021.06.15 |
|---|---|
| [알고리즘] MST 알고리즘 (1) - 그래프 분할 (cut property) (0) | 2021.06.14 |
| [알고리즘] LSD vs MSD in Radix sort (기수 정렬) / C++ 구현 (0) | 2021.06.12 |
| [알고리즘] DFS (Depth-First Search) / C++ 구현 (0) | 2021.06.10 |
| [알고리즘] BFS ( Breadth-First Search) / C++ 구현 (0) | 2021.06.10 |
| [자료구조 ] Tree(트리) 필수 개념, 트리 순회 (0) | 2021.05.22 |
| [알고리즘] Run-Length Encoding (런-렝스 부호화) 쉽게 이해하기 (0) | 2021.05.19 |
![[알고리즘] 계수 정렬 (key-indexed counting sort) / C++ 구현](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FCj0w7%2Fbtq65dM1sXd%2FQQsWuU8LzUXSfs50tWQ3pk%2Fimg.png)