1. BFS란?
BFS는 Breadth-First Search 의 줄임말로 “너비 우선 탐색"이라고 부른다.
BFS의 가장 큰 특징은 layer의 순서대로 탐색한다는 것이다. 즉, 탐색을 시작하는 지점인 root node에서 가까운 순서대로 탐색을 수행한다.
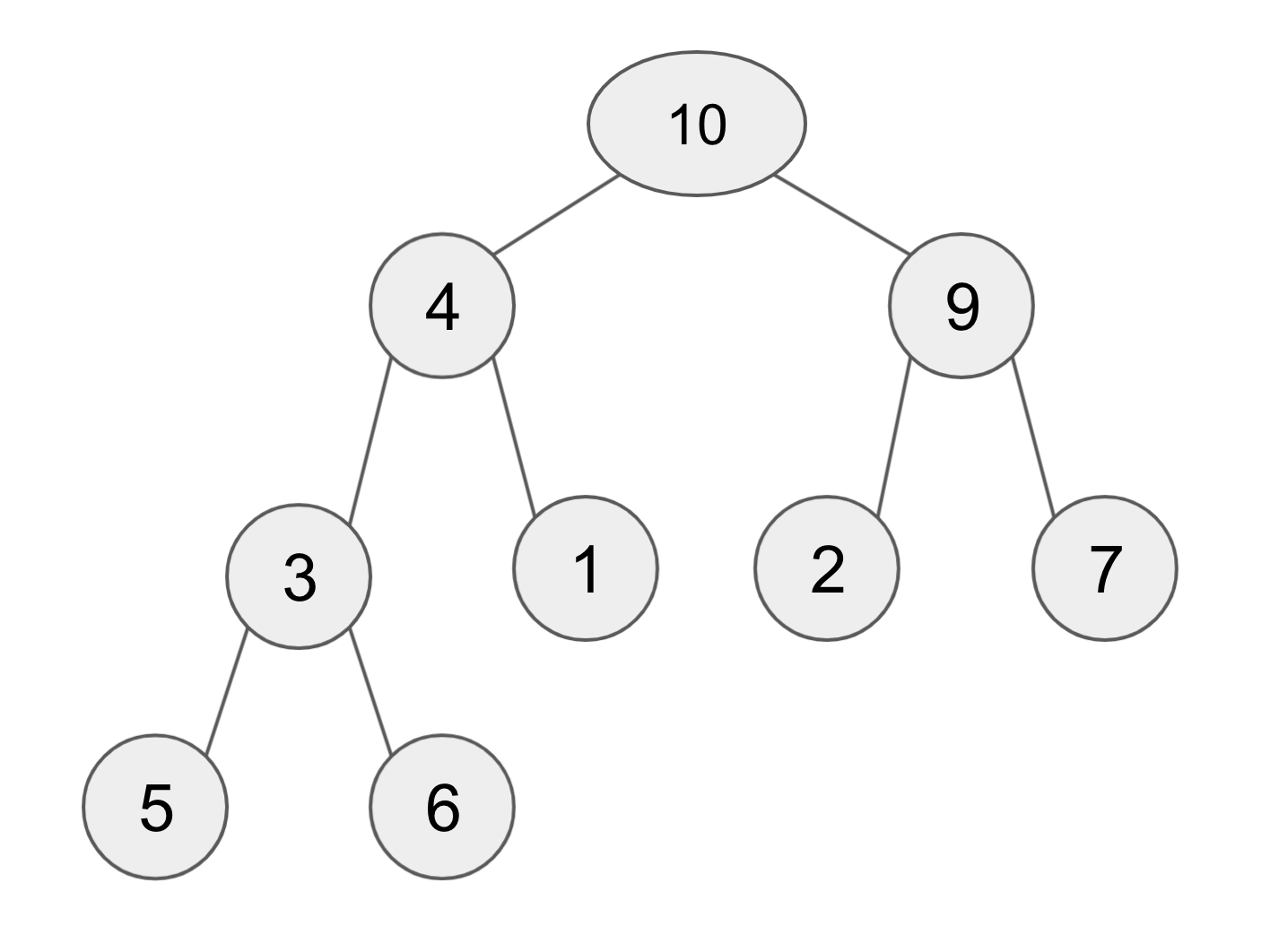
예시로 든 다음 트리에서 1층 레이어에 10, 2층 레이어에 4와 9, 3층 레이어에 3과 1과 2와 7, 마지막 4층 레이어에 5와 6으로 이루어져 있는 것을 볼 수 있다.
BFS는 이 레이어의 층 수 대로 한 층씩 내려오면서 탐색하는 방법을 뜻한다.
결국 위 트리의 BFS 순회는 다음과 같다.
layer-1 layer-2 layer-3 layer-4

Queue를 이용한 리스트로 구현한 BFS에서 N이 모든 Node의 개수이고, M은 Node를 모두 탐색하기 위한 Edge의 개수 일 때, 단지 Node들과 필요한 Edge를 한번씩 방문하면 되기 때문에 시간 복잡도는 다음과 같다.
O(|V| + |E|)
2. BFS가 탐색하는 원리
설명을 위해, 위의 트리를 다음과 같이 인덱스로 놓고 보겠다.
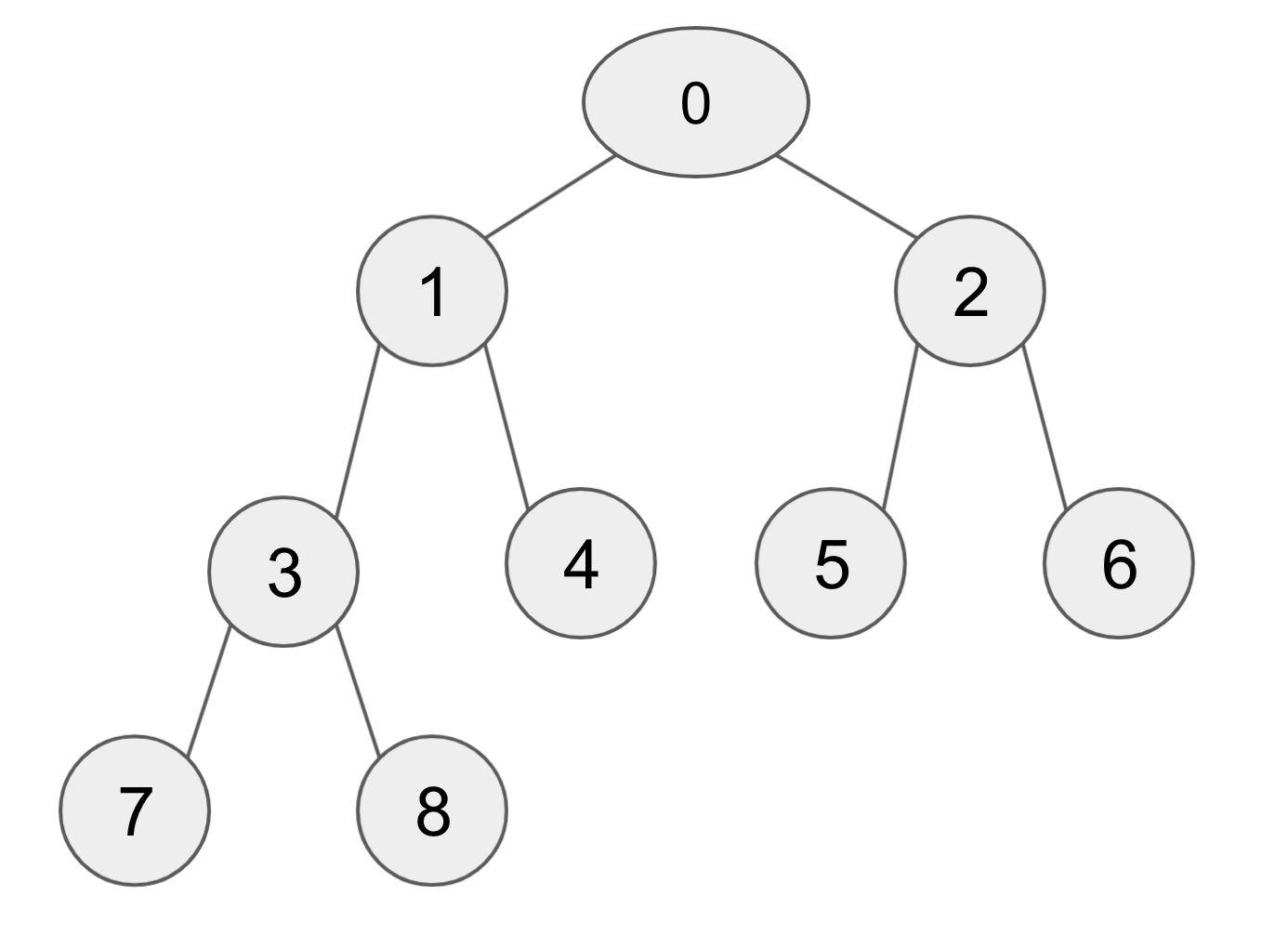
여기서 맨 처음에 queue에는 0이 들어가게 되고, isVisited[0]은 true가 된다.
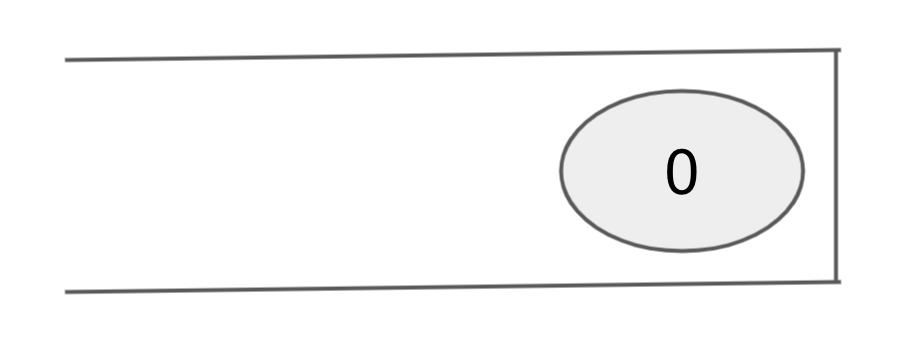
이제 while문으로 들어간다.
여기서는 0이 pop 되고, 0에 연결된 1과 2가 차례로 들어간다.
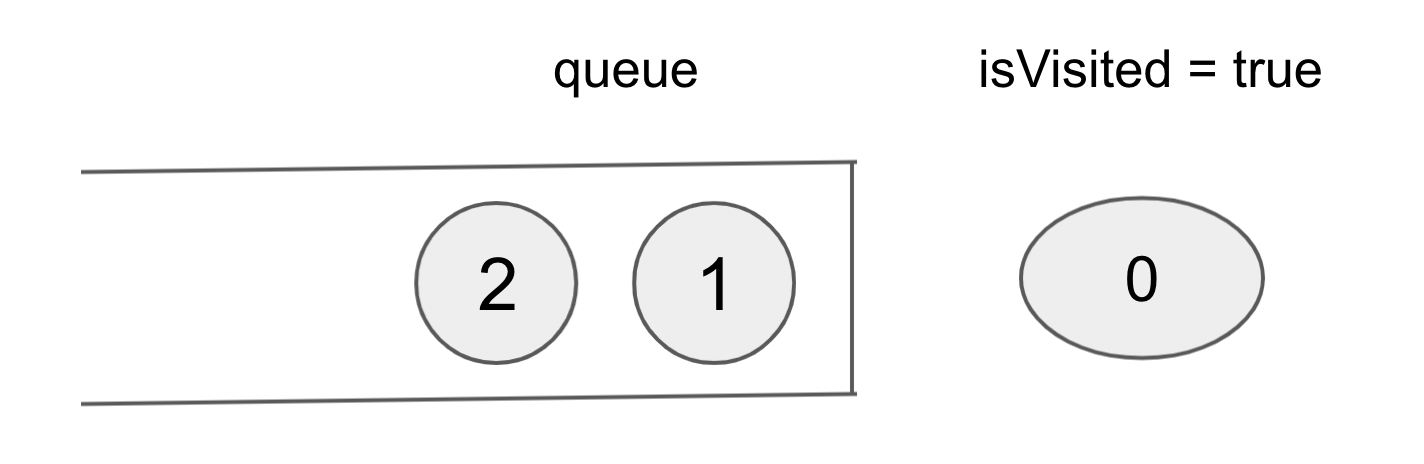
while 문이 돌아가면서,
1이 pop 되고, 1에 연결된 3과 4가 들어간다.
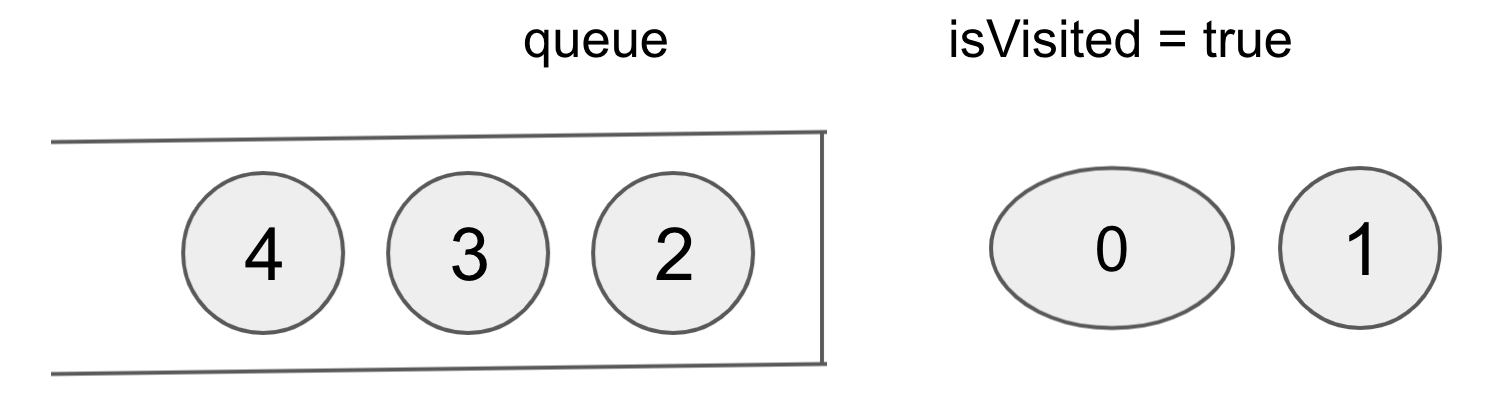
이 다음은 2가 pop 되고, 2와 연결된 5와 6이 들어간다.
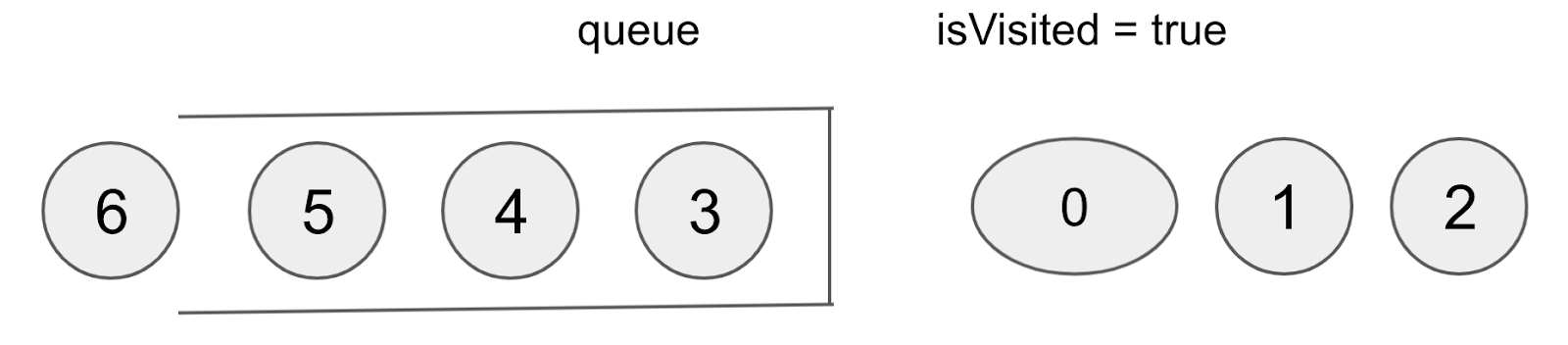
이 다음은 3이 pop 되고, 3과 연결된 7과 8이 들어간다.

이제 큐에 남아있는 4, 5, 6, 7 모두 더 연결되어 있는 edge가 없기 때문에 그냥 pop 되기만 한다.

3. BFS 구현
본 프로그램은 Mac OS 10.15.7 에서 테스트 완료 되었으며, 테스트 컴파일은 C++ 17로 완료하였다.
터미널 컴파일 명령어는 다음과 같다.
clang++ -std=c++17 -o DFS_BFS DFS_BFS.cpp
프로그램 실행은 반드시 노드의 개수 인자를 하나 포함해서 실행해야 한다.
./DFS_BFS [생성하고 싶은 노드의 개수]
[실행 예시]
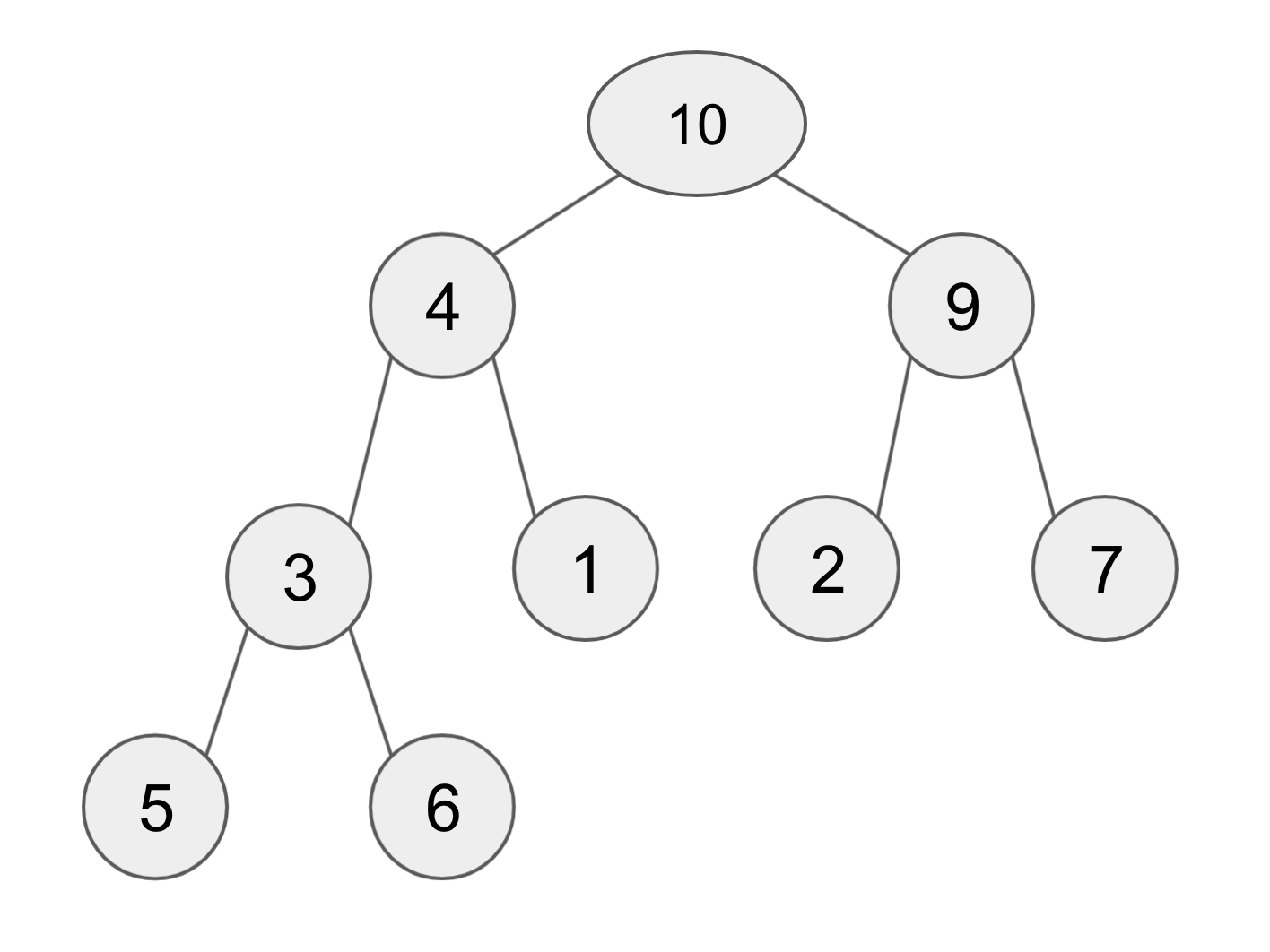
다음 트리의 경우
1. 프로그램 실행 명령어
./DFS_BFS 9
2. key 값 넣기
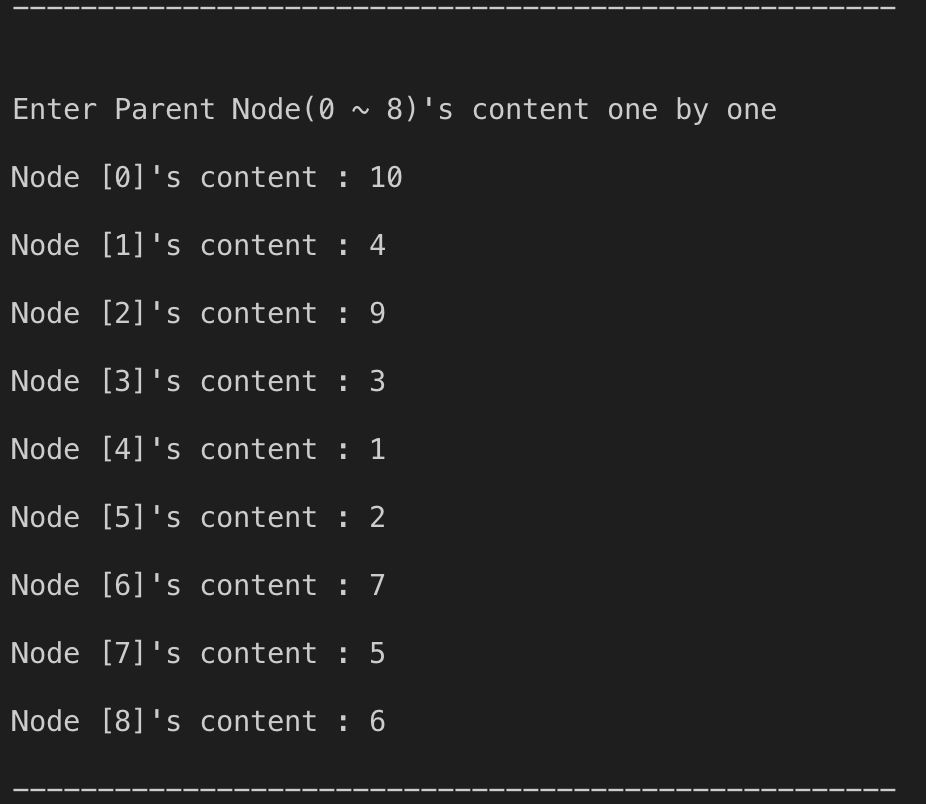
3. Edge 설정하기 (Edge 입력을 끝내고 싶으면 ctrl-D를 입력하면 설정이 완료됩니다.)
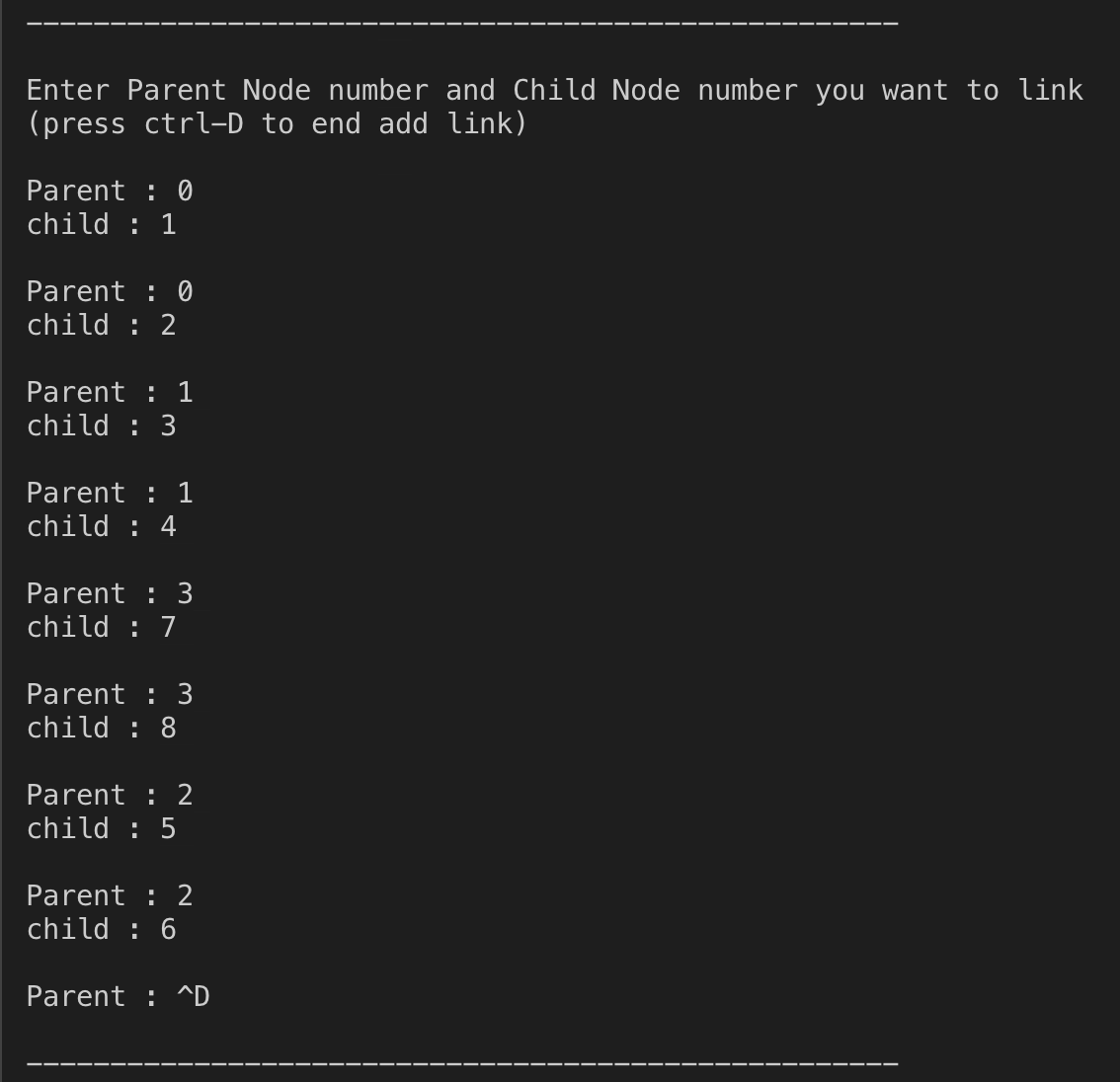
4. 결과 출력
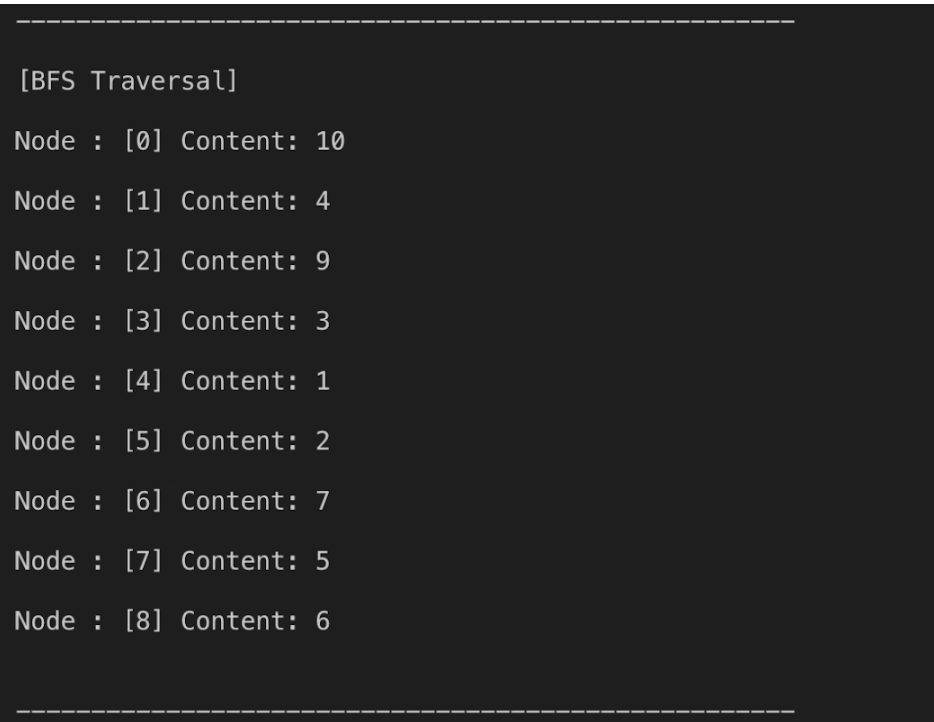
[코드]
#include <iostream>
#include <list>
#include <algorithm>
using namespace std;
class Tree
{
int TreeSize;
list<int> *Nodes; // 노드의 인덱스
list<int> *contents; // 노드의 콘텐츠, 인덱스 마다 1대1 대응이 된다.
public:
Tree(int InputSize);
int setContent(int node, int content);
int setEdge(int parent, int child);
//BFS
void BFS();
void BFSTraversal(list<int> queue, bool *isVisited);
};
/*
** 생성자
*/
Tree::Tree(int InputSize)
{
this->TreeSize = InputSize;
this->Nodes = new list<int>[InputSize];
this->contents = new list<int>[InputSize];
}
/*
** Node의 Content 추가
*/
int Tree::setContent(int node, int content)
{
if (contents[node].size() != 0)
{
cout << "Node [" << node << "] already has one content (command cancled)" << endl;
return (0);
}
this->contents[node].push_back(content);
return (1);
}
/*
** Node의 Link 추가
*/
int Tree::setEdge(int parent, int child)
{
Nodes[parent].push_back(child);
return (1);
}
/*
** BFS 순회
*/
void Tree::BFS()
{
list<int> queue;
bool *isVisited;
int temp;
isVisited = new bool[TreeSize];
for (int idx = 0; idx < TreeSize; idx++)
{
isVisited[idx] = false;
}
BFSTraversal(queue, isVisited);
}
void Tree::BFSTraversal(list<int> queue, bool *isVisited)
{
list<int>::iterator iter;
int this_idx;
isVisited[0] = true;
queue.push_back(0);
while (!queue.empty())
{
this_idx = queue.front();
cout << "Node : [" << this_idx << "] " << "Content: " << contents[this_idx].front() << endl << endl;
queue.pop_front();
for (iter = Nodes[this_idx].begin(); iter != Nodes[this_idx].end(); ++iter)
{
if (!isVisited[*iter])
{
isVisited[*iter] = true;
queue.push_back(*iter);
}
}
}
}
/*
** 실행(실행할 때 매개변수로 전체 사이즈를 넣어야 함.)
*/
void start(int size)
{
// 개수만큼 동적할당
Tree tree(size);
int temp;
int parent;
int child;
// 각각의 노드에 들어가는 값을 할당
cout << "----------------------------------------------------" << endl;
cout << endl;
cout << endl << "Enter Parent Node(0 ~ " << size - 1 << ")'s content one by one" << endl;
for (int idx = 0; idx < size; idx++)
{
cout << endl;
cout << "Node [" << idx << "]'s content : ";
cin >> temp;
if (!tree.setContent(idx, temp))
idx--;
}
cout << endl;
cout << "----------------------------------------------------" << endl;
cout << endl;
// link 할당
cout << "Enter Parent Node number and Child Node number you want to link" << endl;
cout << "(press ctrl-D to end add link)" << endl;
while (true)
{
cout << endl;
cout << "Parent : ";
cin >> parent;
if (cin.eof())
{
cout << endl;
break ;
}
cin.clear();
cout << "child : ";
cin >> child;
if (cin.eof())
{
cout << endl;
break ;
}
cin.clear();
tree.setEdge(parent, child);
}
cout << endl;
cout << "----------------------------------------------------" << endl;
cout << endl;
// BFS 실행
cout << "[BFS Traversal]" << endl << endl;
tree.BFS();
cout << endl;
cout << "----------------------------------------------------" << endl;
}
int main(int argc, char **argv)
{
int size;
if (argc != 2)
{
cout << "ARG ERROR" << endl;
cout << "Enter the number of nodes in the tree when running the program" << endl;
return (1);
}
for (int idx = 0; idx < strlen(argv[1]); idx++)
{
if (argv[1][idx] < '0' || argv[1][idx] > '9')
{
cout << "ARG ERROR" << endl;
cout << "Enter the number of nodes in the tree when running the program" << endl;
return (1);
}
}
size = atoi(argv[1]);
start(size);
return (0);
}
'알고리즘' 카테고리의 다른 글
| [알고리즘] P, NP (0) | 2021.06.15 |
|---|---|
| [알고리즘] MST 알고리즘 (1) - 그래프 분할 (cut property) (0) | 2021.06.14 |
| [알고리즘] LSD vs MSD in Radix sort (기수 정렬) / C++ 구현 (0) | 2021.06.12 |
| [알고리즘] 계수 정렬 (key-indexed counting sort) / C++ 구현 (0) | 2021.06.12 |
| [알고리즘] DFS (Depth-First Search) / C++ 구현 (0) | 2021.06.10 |
| [자료구조 ] Tree(트리) 필수 개념, 트리 순회 (0) | 2021.05.22 |
| [알고리즘] Run-Length Encoding (런-렝스 부호화) 쉽게 이해하기 (0) | 2021.05.19 |
![[알고리즘] BFS ( Breadth-First Search) / C++ 구현](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbU85TB%2Fbtq6Z8LhQyT%2F6dssIAwN0aWHZA57VQsAmK%2Fimg.png)